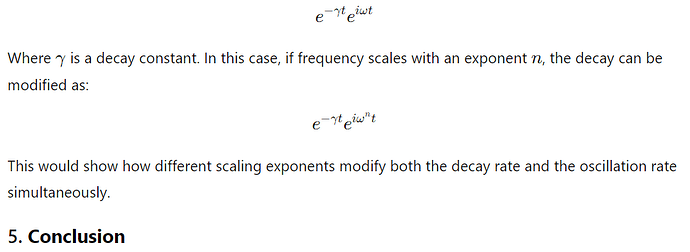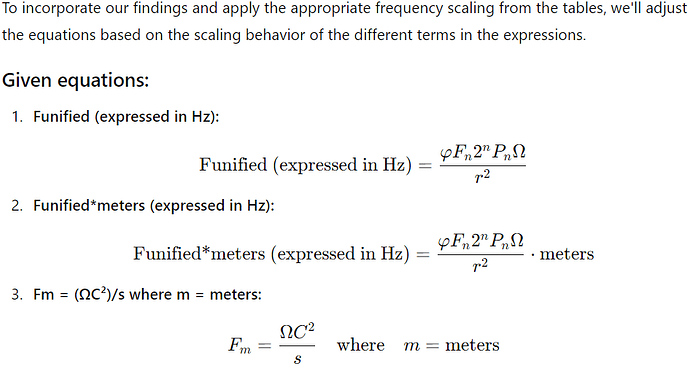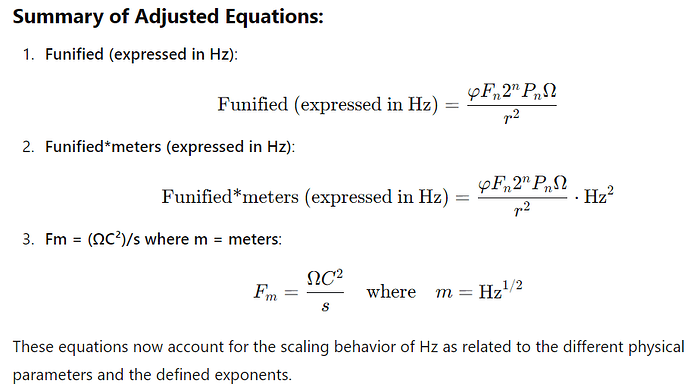PROMPT:
As we revolve around Euler’s, does Hz scaling relate well, or even as expressed in an equation?
Thus, Hz scaling is fundamentally related to Euler’s framework in how it affects oscillations, exponential growth/decay, and wave-like behavior in a system. The scaling of fff (or Hz) in terms of powers or fractions directly impacts how the sinusoidal terms evolve, affecting both the amplitude and frequency of oscillations.
The scaling is connected to higher-order behaviors (as seen with quadratic, cubic, or fractional exponents), and negative exponents represent decay or slower oscillations. Combining these concepts in a unified equation (like we derived earlier) ensures that we account for both linear and non-linear frequency effects.
PROMPT:
build out our tables and equations owing to your last message
PROMPT:
The resultant below equations then become?
Funified (expressed in Hz) = (ϕFn2^nPnΩ)/(r^2)
Funified*meters (expressed in Hz) = (ϕFn2^nPnΩ)/(r^2)(meters)
Fm = (ΩC²)/s where m = meters